Onchain Structured Credit

Pricing Correlation and Jump Risk in Over-Collateralized Crypto Loans

In traditional finance, the spread on a collateralized debt obligation (CDO) compensates investors for the chance that a bunch of seemingly independent assets will default together when the world turns bad. Over-collateralized crypto loans work on the same principle. Each borrower is oversecured and the system as a whole is robust until correlations spike, liquidity dries up, and everyone scrambles to liquidate at once. In this sense, the spread on crypto lending (or the implied CDS premium) is the price of liquidation correlation and jump risk.

Modeling that risk is tricky: Gaussian assumptions miss jump events, correlations are state-dependent, and liquidation mechanics can fail under stress. Yet, even accounting for those limitations, the data point to an attractive equilibrium, roughly 5% yields for blue-chip ETH/BTC loans at 80% liquidation thresholds, and 7–8% for altcoin baskets at 95%. In a world of stretched equity valuations and compressed bond yields, these instruments can help investors form a new, high-quality yield sleeve in their diversified portfolios.

Over-Collateralized Crypto Loans

The cleanest way to explain yield on over-collateralized crypto loans is to start with how traditional structured credit works and then add the crypto-specific frictions that make the numbers what they are. The classic example is mortgage securitization, where each homeowner is a risky micro-exposure; a pool of them is tranched into senior and junior claims. The less subordination you have, the more losses you take when the pool has correlated problems, e.g. a housing downturn in multiple regions.

Crypto lending is not identical, but the analogy is close enough to be useful: each borrower / token looks like a micro “mortgage,” and the protocol’s liquidation LTV (Loan-to-Value Ratio) plays a role very much like a tranche’s attachment point (the minimum of pool-level losses at which a given tranche becomes liable for losses). The pool here is not driven by idiosyncratic default in the mortgage sense; it is driven by market moves hitting the collateral value plus frictions during liquidation.

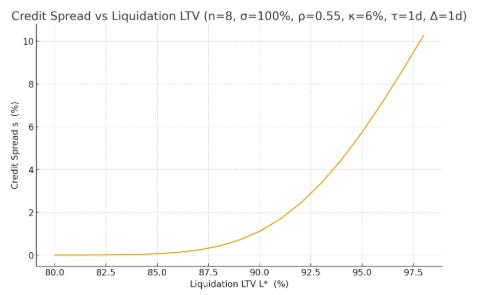
Once you see it this way, spreads for over-collateralized loans should rhyme with MBS/CDO spreads: modest for very safe attachment (e.g., blue-chip collateral with a thick cushion) and larger for thin protection (e.g., high LTV on volatile alt baskets), with the shape of the premium governed by common-factor risk.

Risk Premium Framework

To keep the math where it adds information rather than getting in the way, we compress the pool’s market risk into a single volatility number that already includes correlation. If the assets in collateral each have annualized volatility σ and average pairwise correlation ρ, and the basket is reasonably diversified with n names and roughly equal weights, the collateral portfolio’s volatility is

\(\sigma_p \;=\; \sigma\sqrt{\rho+\frac{1-\rho}{n}}. \)

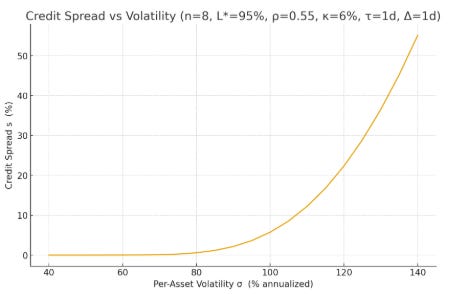
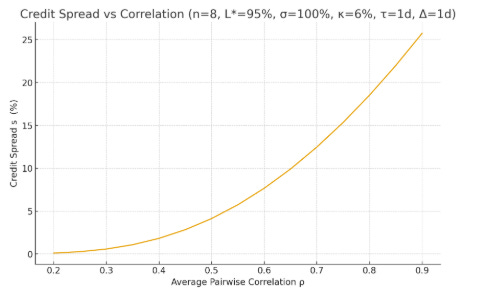
This expression is a useful because it says diversification kills idiosyncratic noise but leaves a correlation floor of σ times the square root of ρ​. That floor is what senior mortgage tranches “see” when the housing market turns together, and it is what safe crypto loans “see” when BTC, ETH, and altcoins lurch in the same direction. Because expected losses in risk-neutral pricing scale with volatility and the frequency of hitting a liquidation threshold, σ of the aggregate collateral portfolio ​is the natural bridge from “how correlated/volatile is the basket?” to “what spread is fair?”

The liquidation mechanics matter, but we can summarize them in two short statements. First, triggers are not losses: hitting the liquidation LTV simply starts the unwind. Second, losses come from the time and cost of that unwind, because prices can continue to fall and you pay slippage, fees, and market impact. A compact risk-neutral identity captures everything we need:

\( s \;=\; \lambda_{\mathrm{hit}} \, \overline{L}_{\mathrm{hit}} \)

Here s is the par “CDS premium” for the loan (economically, the loan’s credit spread); λ is the hazard—how often the collateral breaches the barrier; and L​ is the expected fractional loss given that liquidation is triggered. In standard credit language, this is simply frequency × severity. If the coupon spread on the loan equals s, then buying CDS on the loan leaves you with the risk-free rate r in expectation.

Risk Calculations Outline

For readers who want to see the pieces: consider a risk interval Δ (think oracle cadence), the portfolio log return is approximately normal with mean & variance

\(\mu_{\Delta} = (r - \tfrac{1}{2}\sigma_p^{2})\,\Delta, \qquad \sigma^2_{\Delta} = \sigma_p^{2}\,\Delta \)

The “one-step” probability of breaching the liquidation barrier is therefore

\(p_{\mathrm{hit}}(\Delta) =\Phi\!\left( \frac{\ln(LTV_0/L^\*)-\mu_{\Delta}} {\sigma_p\sqrt{\Delta}} \right)\)

where L\* denotes the LTV threshold for liquidation; and the per-year trigger intensity is well-approximated by

\(\qquad \lambda_{\mathrm{hit}} \approx -\frac{\ln(1-p_{\mathrm{hit}})}{\Delta}\)

After a trigger, liquidating takes time τ and costs a fraction κ. Over τ, the log return is Y roughly normal and distributed on

\(Y \;=\; \ln\!\Big(\frac{V_{t+\Delta+\tau}}{V_{t+\Delta}}\Big) \sim \mathcal N\!\big(\mu_\tau,\sigma_p^2\tau\big), \qquad \mu_\tau = \big(r-\tfrac{1}{2}\sigma_p^2\big)\tau\)

Conditioning on the trigger and integrating the truncated lognormal, the expected loss severity has a closed form described by a very ugly integral, which we leave as an exercise for the reader. In any case the market inputs are σ of the portfolio and the risk free rate r; the protocol dials are the liquidation LTV given by L\*, the initial operating LTV0​, the unwind time τ, and the all-in cost κ for the liquidator.

Core Results & Graphs

With the above framework in hand, we can analyze the risk-neutral CDS spreads of various over-collateralized loan protocols.

Take a blue-chip dominant BTC/ETH basket on Aave for example with portfolio volatility is 40%. If borrowers are run at a prudent LTV0 = 70% with liquidation at L\*=80%, hourly checks Δ=1/12 (in reality much more often) and an unwind time of τ=1/12 with total liquidation cost κ=3%, the combination of a thick cushion and small τ and κ makes triggers rare and post-trigger losses even rarer.

These parameters produces spreads that round to zero at risk-neutral expectations. That’s why a low spread like 50 bp for jump/oracle/operational tail risk is enough to justify ≈5% total yield when the cash rate is 4.5%.

Altcoin lending on slower vaults is more akin to mortgage equity analogue. For example, if you lend on Jupiter or Kamino, chances are that you are able to lend against much more volatile collateral with LTV pushing 95%+.

Below we have some graphs showing credit sensitivity to different parameters

While an interest rate strategy that describes the true equilibrium expected returns for any given level of risk should naturally be smooth, the piecewise linear models employed by most lending protocols is a decent approximation.

It is important not to oversell a Gaussian, diffusion-based view in crypto. Traditional MBS modeling famously leaned on Gaussian copulas for correlation across mortgages, which captured average co-movement but missed tail dependence. In crypto, the case against pure Gaussians is stronger; exchange outages and forced liquidations and can create single-interval drops that dominate the diffusion. A Gaussian copula with constant ρ will underprice tail risk for thin-cushion loans in precisely the same way the pre-GFC models underpriced mezzanine tranches.

Even with a realistic jump term, however, senior structures with genuine over-collateralization should nonetheless still be robust to modeling details while thinner structures should “feel” your tail assumptions.

Implications for Allocation

From a portfolio perspective, over-collateralized crypto loans are a new species of structured yield: they monetize correlation and liquidity risk rather than credit or duration risk. The carry comes from liquidation covariance—a payoff stream largely orthogonal to equities and only weakly linked to traditional credit spreads. For allocators, this makes them a useful source of uncorrelated income at a time when most risk premia are compressed.

At the senior end, BTC/ETH loans with 75–80% liquidation thresholds resemble AAA securitized tranches: short-duration, self-liquidating, transparent, and yielding about 5% when the risk-free rate is 4.5%. The expected losses under diffusion dynamics are near zero, and the yield compensates mainly for operational and tail liquidity risk. For treasuries or stablecoin funds seeking a cash-plus alternative, this offers high real yield without duration—a rare combination in the current macro regime.

The altcoin and mixed-asset loans, typically 90–95% LTV and yielding 7–9%, function as mezzanine structured credit: they pay investors for thin protection and for the fact that correlation and liquidation costs spike together in stress. Their risk is liquidity-cyclical rather than macro-cyclical, so returns are imperfectly correlated with corporate credit or equities.

At the portfolio level, a 5–10% allocation to these loans can lift portfolio yield by roughly 50–100 bps while improving convexity: losses occur in brief liquidity shocks, not in slow macro drawdowns. Their short-tenor, on-chain mark-to-market design limits hidden leverage and duration drag, and the yield premium—essentially a correlation risk premium—is the type of spread that tends to compress as markets mature. In a world of overvalued equities and capped real rates, crypto-secured lending behaves like a new short-duration structured-income asset class: high Sharpe, low beta, and one of the few yield sources not already owned by every 60/40 portfolio.

Disclaimer

The information provided on TheLogbook (the “Substack”) is strictly for informational and educational purposes only and should not be considered as investment or financial advice. The author is not a licensed financial advisor or tax professional and is not offering any professional services through this Substack. Investing in financial markets involves substantial risk, including possible loss of principal. Past performance is not indicative of future results. The author makes no representations or warranties about the completeness, accuracy, reliability, suitability, or availability of the information provided.

This Substack may contain links to external websites not affiliated with the author, and the accuracy of information on these sites is not guaranteed. Nothing contained in this Substack constitutes a solicitation, recommendation, endorsement, or offer to buy or sell any securities or other financial instruments. Always seek the advice of a qualified financial advisor before making any investment decisions.